

A bag contains 4 white and 6 blue balls. If a ball is drawn at random, the probability that the drawn ball to blue is:
3/5
If a coin is tossed twice, the probability of getting at least one head is
3/4
The distance of a point (3, 3) from x-axis is
3 units
If an angle is 3 times its complementary angle, then the measure of the angle is
67.5°
If an angle of a parallelogram is four times of its adjacent angle, then these two angles of the parallelogram are
144°, 36°
Two sides of a triangle are 5 cm and 9 cm. Which of the following length can be the length of the third side?
13 cm
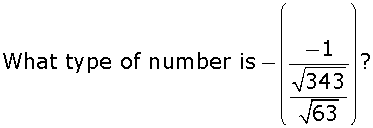
Positive rational number
Which of the following is a factor of the polynomial 2t4 + 3t3 – 2t2 – 9t – 12?
t2 – 3
The length of the chord of a circle is 30 cm and its distance from the centre is 8 cm. Then, the radius of the circle is
17 cm
Mode of data 24, 17, 13, 24, 26, 20, 26, 30, 8, 41, 24 is
24
Let the sides of a triangle be 4 cm, 7 cm and 11 cm, then area of the triangle is_____ cm2.
In geometrical figures, sides decide sizes and _____ decide shapes.
In geometrical figures, sides decide sizes and angles decide shapes.
An algebraic expression in which the variables involved have only non-negative integral powers is called a _________.
An algebraic expression in which the variables involved have only non-negative integral powers is called a polynomial.
The number of circle passing through three non-collinear points is ____.
The number of circle passing through three non-collinear points is one.
On comparing 4x – 17 = 23 y with ax + by + c = 0, the value of a + b + c is _____.
The given equation, 4x – 17 = 23 can be written as 4x – 23y – 17 = 0.
On comparing this equation with ax + by + c = 0, we
get, a = 4, b = – 23 and c = – 17
Then, a + b + c = 4 + (– 23) + (– 17)
= 4 – 40
= – 36
On comparing 4x – 17 = 23y with ax + by + c = 0, the value of a + b + c is –36.
If the graph of a polynomial y = p(x) intersects the x-axis at three points, then what is the number of zeros of p(x)?
The number of zeros is 3, as the graph intersects the x-axis at three points.
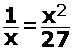 , then find x is rational or irrational number.
, then find x is rational or irrational number.There are 4 kings in a deck of cards. Let E be the event of the card which is a king.
The number of outcomes favourable to E = 4
The number of possible outcomes = 52
Therefore,
P(a king) = (4/52)
= 1/13.

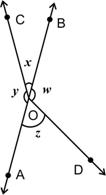
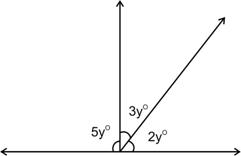
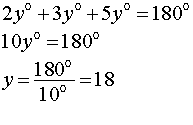
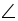 POR :
POR : 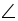 ROQ = 5 : 7, find all the angles.
ROQ = 5 : 7, find all the angles. 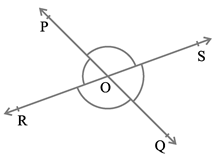
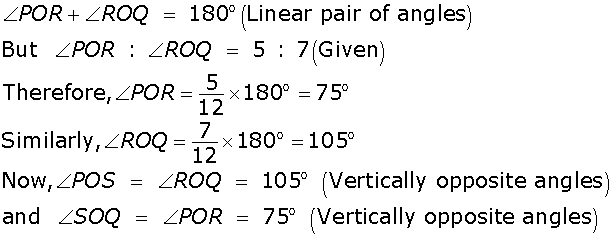
Find the zeros of polynomial 2x2 - 8.
2x2 - 8 = 0
⇒ 2x2 = 8
⇒ x2 = 4
⇒ x = 2 and -2
Hence, 2 and -2 are the zeros of the polynomial.
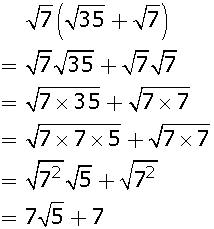
Inner radius of well (r) = 8/2 m
= 4 m
Width of embankment = 3 m
Radius of well with embankment (R) = 4 + 3 = 7 m
Depth of well = 21 m
Volume of earth taken out from well =  r2h
r2h
= (22/7)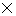 (4)2
(4)2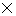 21
21
= 22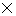 16
16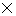 3
3
= 1056 m3
Area of embankment = 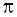 (R2 - r2)
(R2 - r2)
= (22/7)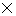 {(7)2 - (4)2}
{(7)2 - (4)2}
= (22/7)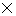 11
11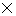 3
3
= (726/7) m2
Height of embankment = (Volume of earth taken out from well)
(Area of embankment)
= 1056 / (726/7)
= (1056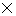 7)
7)
726
= 10.2 approx.
Area of quadrilateral ABCD = (area of  ABD+ area of
ABD+ area of  CDB)
CDB)
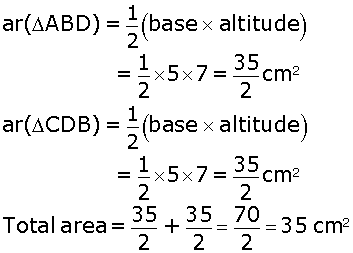
Hence, area of quadrilateral ABCD = 35 cm2.
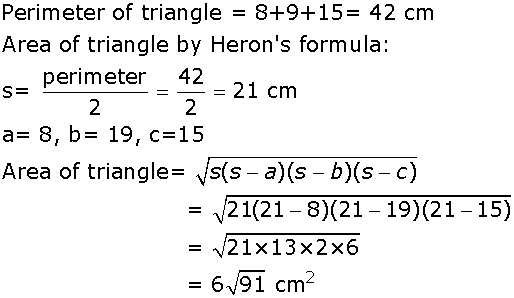
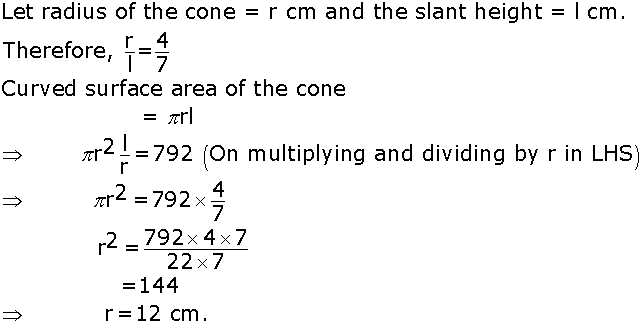
Factorise:
![]()
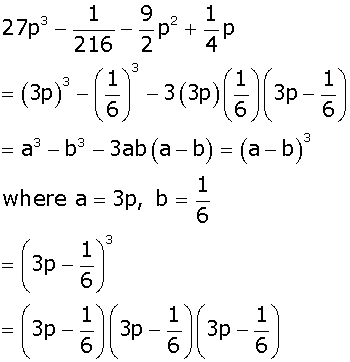
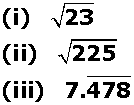
(i) ![]() = 4.79583 ……. [By square root method]
= 4.79583 ……. [By square root method]
Which is non- terminating and non -recurring.
SO, by the decimal - expansion property of irrationals, ![]() is irrational.
is irrational.
(ii) ![]() Which is terminating.
Which is terminating.
SO, by the decimal expansion property of rational, ![]() is rational.
is rational.
(iii) By the decimal expansion property of rational, ![]() is rational.
is rational.
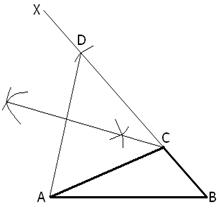
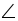 B=60
B=60
To Construct:-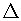 ABC
ABC
Step 1. Draw a line segment AB 5.8 cm

Since 1 kg.=1000 gm
So, the weight of one cubic cm of wood is 62.89 gm and one cubic cm of sand is 101.01 gm.

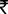
Let the cost of 1 kg apples be 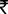 x and the cost of 1 kg grapes be
x and the cost of 1 kg grapes be 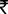 y.
y.
According to the question, linear equation is
5x = 150 +7y
5x – 7y =150
It is the required equation.
Since the cost of one kg grapes is 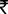 70.
70.
By putting y = 70 in the above equation,
we get
5x – 7(70) = 150
5x = 490 + 150
x = 640/5
= 128
Thus, the cost of 1 kg apples is 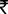 128.
128.
 BCD) = ar(
BCD) = ar( ACD)= 1/2ar(
ACD)= 1/2ar(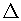 ABC) ...(i) (Median divides the triangle into two triangles of equal areas.)
ABC) ...(i) (Median divides the triangle into two triangles of equal areas.) ar(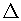 DPQ) = ar(
DPQ) = ar(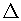 PDC) (Two triangles having same base and between same parallel lines are equal in area.)
PDC) (Two triangles having same base and between same parallel lines are equal in area.)
ar(DPQ) + ar(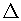 BDP) = ar(
BDP) = ar( PDC)) + ar(BDP)
PDC)) + ar(BDP)
ar( BPQ)= ar(
BPQ)= ar( BCD)
BCD)
ar( BPQ) = 1/2ar(
BPQ) = 1/2ar(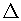 ABC) [ from (i)]
ABC) [ from (i)]



In  PQR, PR>PQ
PQR, PR>PQ
so,  PQR>
PQR> PRQ ...(1) [angle opposite to greater side is greater]
PRQ ...(1) [angle opposite to greater side is greater]
 QPS=
QPS= RPS ...(2) [PS is bisector of P]
RPS ...(2) [PS is bisector of P]
Add  QPS both sides of relation (1), we get
QPS both sides of relation (1), we get
 PQR+
PQR+ QPS>
QPS> PRQ+
PRQ+ QPS
QPS
 PQR+
PQR+ QPS>
QPS> PRQ+
PRQ+ RPS [From equation (2)]
RPS [From equation (2)]
180°- PSQ>180°-
PSQ>180°- PSR [By angle sum property]
PSR [By angle sum property]
- PSQ>-
PSQ>- PSR
PSR
So,  PSR>
PSR> PSQ
PSQ




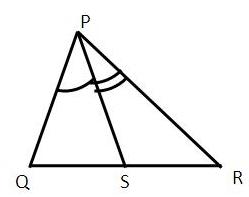
 PQT=
PQT= TQR and
TQR and  PRT=
PRT= TRS
TRS
To Prove:- QTR=(1/2)
QTR=(1/2) QPR
QPR
Proof:-In 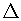 PQR,
PQR,
Ext.
 PRS=
PRS= PQR+
PQR+ QPR
QPR
2 TRS=2
TRS=2 TQR+
TQR+ QPR [Since TQ and TR are angle bisectors]
QPR [Since TQ and TR are angle bisectors]
2( TRS-
TRS- TQR)=
TQR)= QPR
QPR
TRS- TQR=(1/2)
TQR=(1/2) QPR ...(1)
QPR ...(1)
In  TQR,
TQR,
Ext. TRS=
TRS= TQR+
TQR+ QTR
QTR
TRS- TQR=
TQR= QTR ...(2)
QTR ...(2)
from equation (1) and equation (2), we have
 QTR =(1/2) QPR
QTR =(1/2) QPR
It is given that AS = SD = DA
Therefore,  ASD is an equilateral triangle.
ASD is an equilateral triangle.
OA (radius) = 20 m
Medians of equilateral triangle pass through the circumcentre (O) of the
equilateral triangle ASD. We also know that medians intersect each other
in the ratio 2: 1. AB is the median of equilateral triangle ASD,
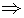 (OA/OB) = 2/1
(OA/OB) = 2/1
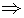 (20/OB) = 2/1
(20/OB) = 2/1
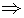 OB = 10 m
OB = 10 m
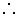 AB = OA + OB = (20 + 10) m = 30 m
AB = OA + OB = (20 + 10) m = 30 m
In 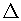 ABD,
ABD, 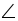 ABD=90
ABD=90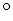 , So by Pythagoras Theorem
, So by Pythagoras Theorem
AD2 = AB2 + BD2
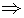 AD2 = (30)2 + (AD/2)2
AD2 = (30)2 + (AD/2)2
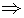 AD2 = 900 + (1/4)AD2
AD2 = 900 + (1/4)AD2
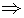 (3/4)AD2 = 900
(3/4)AD2 = 900
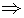 AD2 = 1200
AD2 = 1200
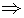 AD = 20
AD = 20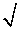 3
3
Therefore, the length of the string of each phone will be 20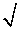 3 m.
3 m.
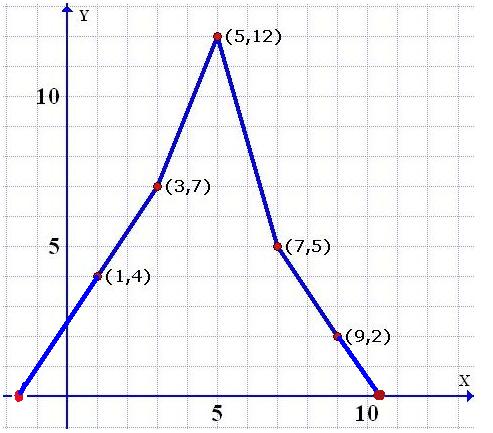
Construct a frequency polygon for the following data:
| Age ( in years) | Class marks | Frequency |
| 0-2 | 1 | 4 |
| 2-4 | 3 | 7 |
| 4-6 | 5 | 12 |
| 6-8 | 7 | 5 |
| 8-10 | 9 | 2 |

Take your CBSE board preparation to another level with AI based and rich media animation on Extramarks - The Learning App.
Features of Learning App