

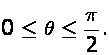
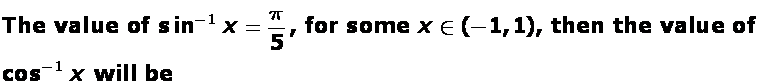

A team of 8 couples(husband and wife) attended a lucky draw in which 4 persons were picked up for a prize. The
probability that at least one couple is selected for the prize is
A bag contains 16 coins of which two are counterfeit with heads on both sides. The rest are fair coins. One is
selected at random from the bag and tossed. The probability of getting a head is
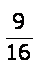
The angle between the line 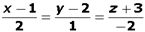 and the plane x + y + 4 = 0 is
and the plane x + y + 4 = 0 is
45°
Let A = {2, 3, 4}, B = {5, 6, 7, 9} and let f = {(1, 4), (3, 6), (4, 7)} be a function from A to B, then function is ______________.
Since, every element of set A has only one image in set B i.e., 2→5, 3→6 and 4→7. Therefore, f is one-one function.
If x = 4at and y = 3at2, then the equation of tangent at t = 2 is _______________.
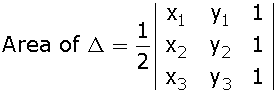
 2 matrix A = [ aij ] whose elements are given by
2 matrix A = [ aij ] whose elements are given by 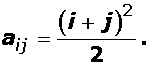
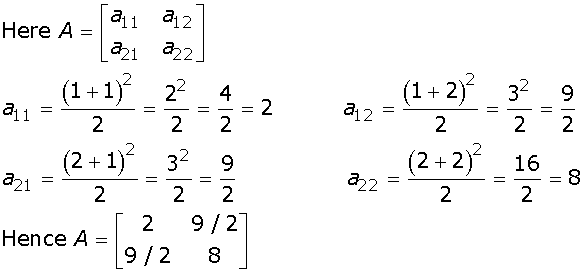
Write 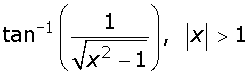 in the simplest form.
in the simplest form.
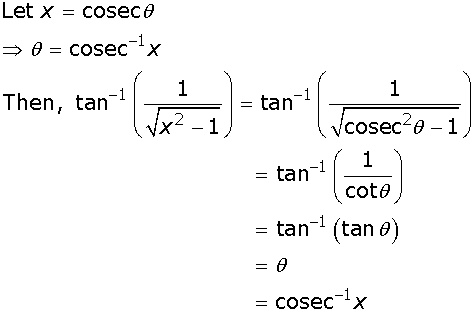
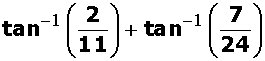 .
.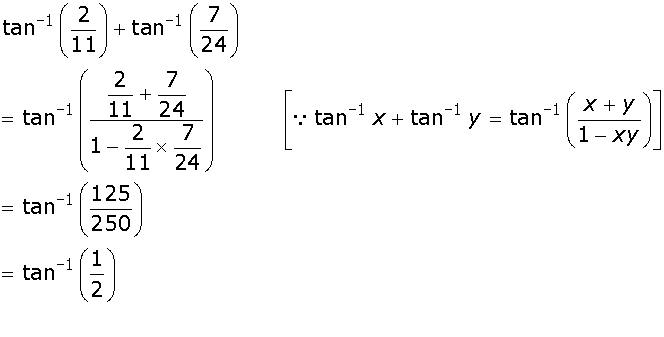
 ABC is isosceles.
ABC is isosceles.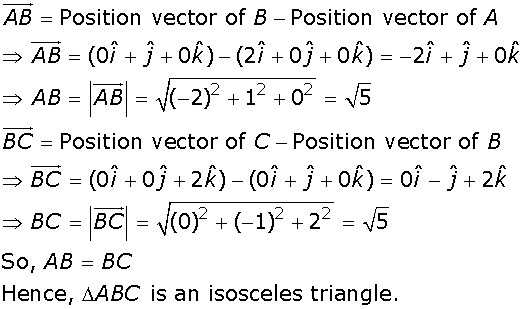
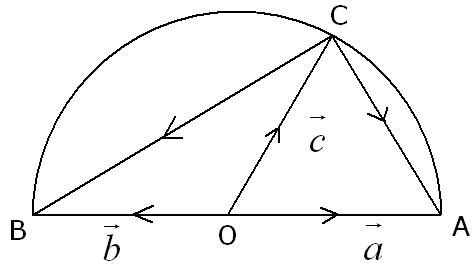
Prove that the angle in a semi-circle is a right angle.
Let C be any point on the semi-circle.
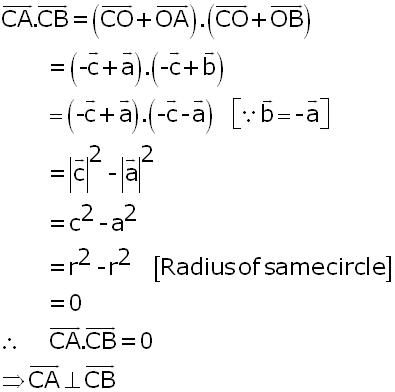

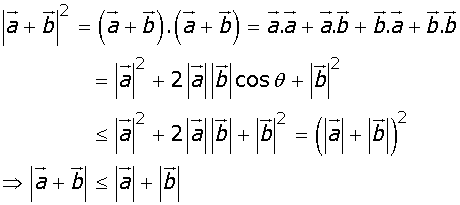
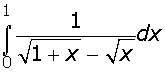 .
.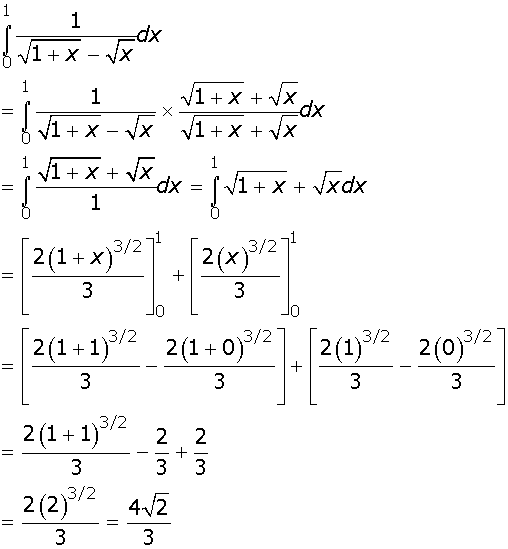
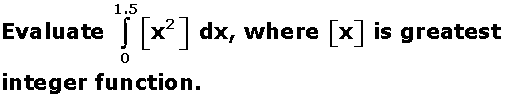
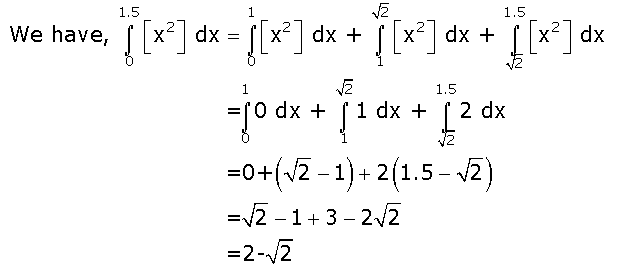
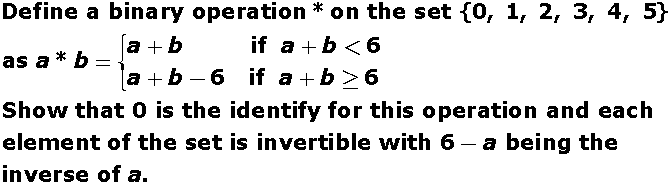

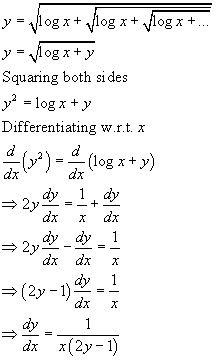
 0.037.
0.037.Let y =  x, x = 0.040 and x +
x, x = 0.040 and x +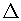 x = 0.037.
x = 0.037.
Then 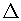 x = 0.037 - 0.047 = - 0.003
x = 0.037 - 0.047 = - 0.003
For x = 0.040, y = 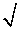 0.040 = 0.2
0.040 = 0.2
Let dx = 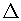 x = - 0.003
x = - 0.003
Now, y = 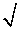 x
x
i.e., dy/dx = 1/2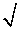 x = 1/0.4.
x = 1/0.4.
Therefore, dy = dy/dx x dx
i.e., dy = (1/0.4) ( - 0.003) = -3/100
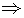
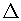 y = -3/400
y = -3/400
Hence, 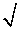 0.037 = y +
0.037 = y + 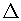 y = 0.2 - (3/400) = 0.1925.
y = 0.2 - (3/400) = 0.1925.
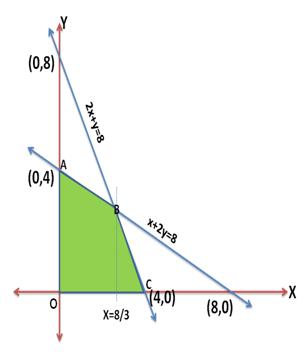
Subject to constraints
x + y 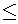 50
50
3x + y 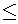 90
90
x, y 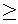 0
0
Subject to constraints
x + y 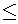 50 (2)
50 (2)
3x + y 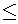 90 (3)
90 (3)
x, y 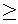 0 (4)
0 (4)
Graph the inequalities (2), (3) and (4). The feasible region (shaded) is shown below:
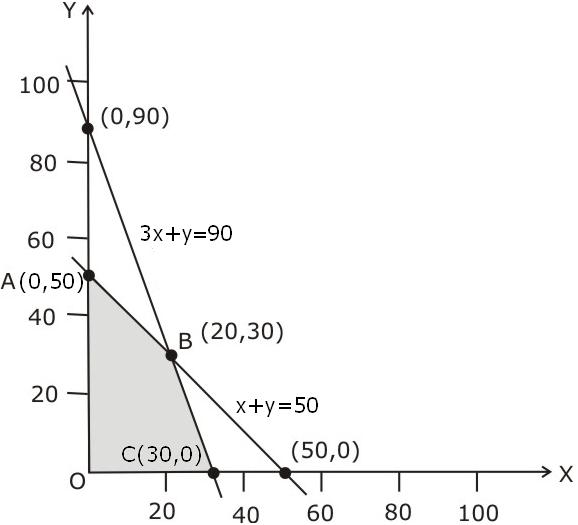
Corner Point Z = 60x +15y A(0, 50) 750 B(20, 30) 1650 C(30, 0) 1800  Maximum
Maximum
The maximum value of Z on the feasible region occurs at x = 30 and y = 0.
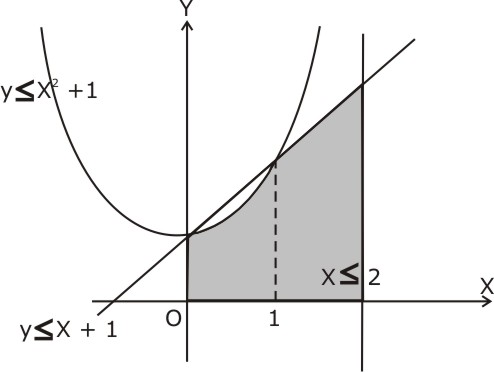
 y
y  x2 + 1, 0
x2 + 1, 0 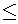 y
y 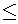 y
y 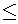 x +1, 0
x +1, 0 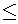 x
x 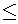 2}.
2}.
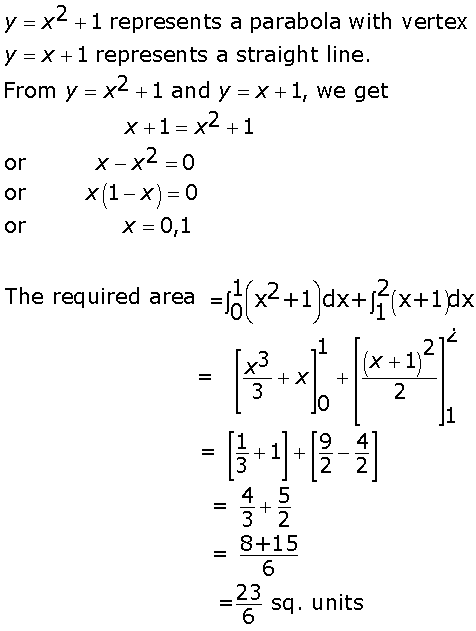


In a class of 60 students, 32 like Maths, 30 like Biology and 24 like both Maths and Biology. If one of these students is selected at random, find the probability that the selected student
(a) likes Maths or Biology
(b) likes neither Maths nor Biology
(c) likes Maths but not Biology.
Let the probability that a student likes Maths be denoted by P(M) and Biology be denoted by P(B).It is given that
P(M) = 32/60 = 8/15, P(B) = 30/60 = 1/2, P(M B) = 24/60 = 2/5
B) = 24/60 = 2/5
(a) Probability that the selected student likes Maths or Biology
P(M B) = P(M) + P(B) – P(M
B) = P(M) + P(B) – P(M B)
B)
= 8/15 + 1/2 - 2/5 = 19/30.
(b) Probability that the student likes neither Maths nor Biology = 1 - P(M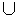 B)
B)
= 1 - 19/30 = 11/30
(c) Probability that a student likes Maths but not Biology = P(M) – P(M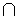 B)
B)
= 8/15 - 2/5 = 2/15.
The target is hit by atleast two persons in the following mutually exclusive ways:
(a) P hits, Q hits and R does not hit i.e., E1 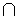 E2
E2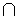 E3c
E3c
(b) P hits, Q does not hit and R hits i.e., E1 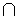 E2c
E2c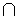 E3
E3
(c) P does not hit, Q hits and R hits i.e., E1c 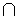 E2
E2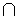 E3
E3
(d) P hits, Q hits and R hits i.e., E1 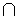 E2
E2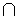 E3
E3
Required Probability = P[(a) 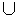 (b)
(b) 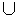 (c)
(c)  (d)] = P(a) + P(b) + P(c) + P(d)
(d)] = P(a) + P(b) + P(c) + P(d)
= (3/4 x 2/3 x 1/5) + (1/4 x 2/3 x 4/5) + (3/4 x 2/3 x 4/5)
= 25/30 = 5/6.


Take your CBSE board preparation to another level with AI based and rich media animation on Extramarks - The Learning App.
Features of Learning App