


Show that the sequence < an> defined by
an =4n+5 is an A.P. also its common difference is
 N), the coefficients of (p+1)th and (p + 3)th terms are equal, then
N), the coefficients of (p+1)th and (p + 3)th terms are equal, then 
In the Venn diagram shown below, (A B
B  C)' =
C)' =
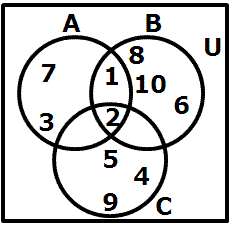
{}.
R = {(0, 0), (0, 1), (1, 1), (2, 1), (2, 2), (2, 0), (1, 0), (0, 2), (0, 1)}
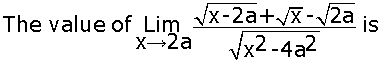
1/2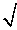 a.
a.
The value of 0! × 2! × 3! is ____.
0! × 2! × 3! = 1× (2 × 1) × (3 × 2× 1)
= 12
The value of 0! × 2! × 3! is 12.
There are 4 elements in a set A and 5 elements in the set B, then there will be ___ elements in A × B.
It is given that n(A) = 4
and n(B) = 5
Therefore, n(A × B) = 4 × 5
= 20
There are 4 elements in a set A and 5 elements in the set B, then there will be 20 elements in A × B.
The imaginary part in (3 + 2i)(1 – 4i) is _____.
(3 + 2i)(1 – 4i) = 3 – 12i + 2i – 8i2
= 3 – 10i – 8(–1)
= 3 – 10i + 8
= 11 – 10i
The imaginary part in (3 + 2i)(1 – 4i) is –10.
The value of i9 – i19 is _____.
i9 – i19 = i4.i3 – (i4)4i3
= 1(–i) – (1)4(–i) [Since i4 = 1 and i3 = - i]
= 0
The value of i9 – i19 is 0.
The derivative of x3(x – 3)2 is ______.
Here,
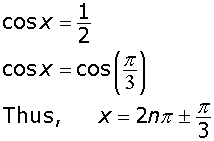
where n is any integer.
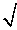 3/2).
3/2). Here,
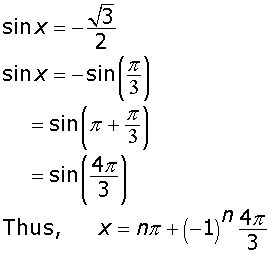
where n is any integer.
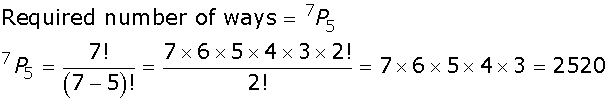
Given that A = 2, B = -5, C1 = 7 and C2 = 5.
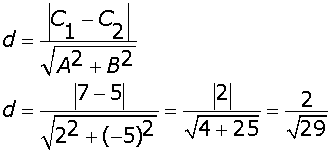
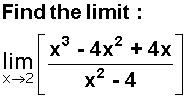
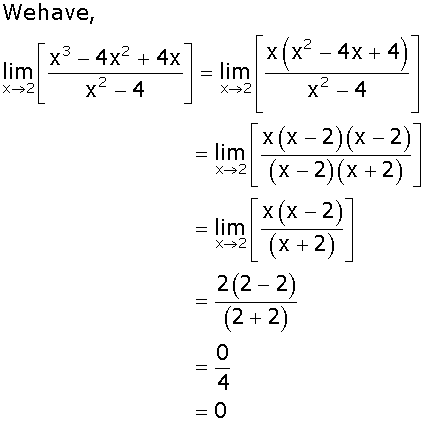
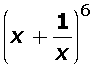 .
.
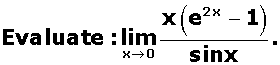
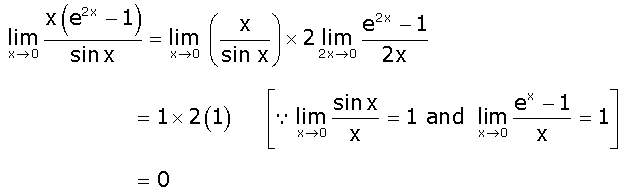
![]()
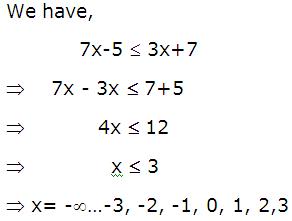
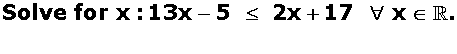
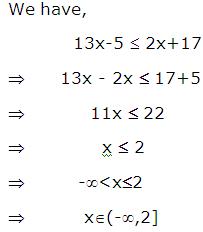
Find the ratio in which the line segment joining the points (4, 8, 10) and (6, 10, -8) is divided by the XZ-plane.

Find the distance between (2, -1, 3) and (-2, 1, 3).
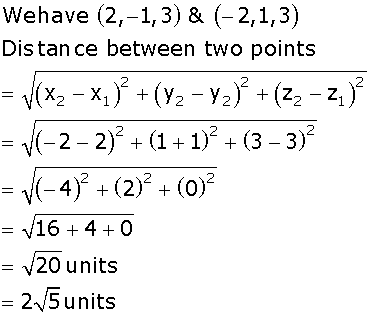
Find the distance of the point (5,-2) from the line 7x - 2y + 3 = 0.
The perpendicular distance (d) of a line Ax + By + C = 0 from a point
(x1 , y1) is given by :
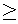 7}
7}1. A' = {x : x is an odd natural number}
2. B' = {x : x 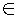 N, x
N, x 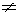 2}
2}
3. C' = {x : x 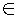 N and x < 7}
N and x < 7}
4. D' = {x : x is a composite number}
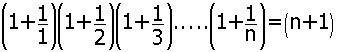 by using principle of mathematical induction.
by using principle of mathematical induction.
If 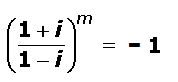 , then find the least positive integral value of m.
, then find the least positive integral value of m.
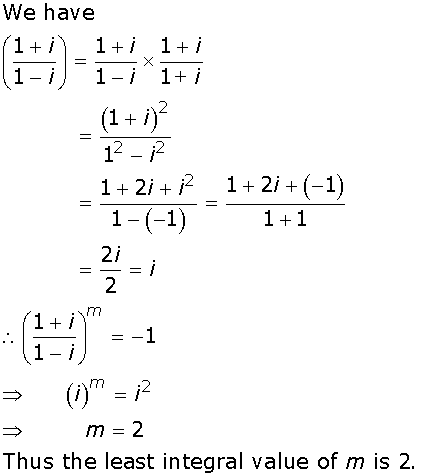
(a) If the 3 students join the excursion party then the number of combinations will be C1= C(12, 7)
(b) If the 3 students do not join the excursion party. Then the number of combinations C2= C(12, 10)
If C is the combination of choosing the excursion party, then
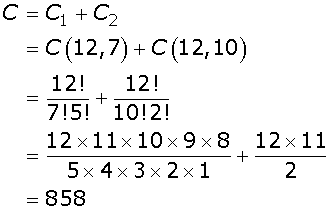
I (5 questions) II (7 question)
(a) 3 5
(b) 4 4
(c) 5 3
If P is the required number of ways, then
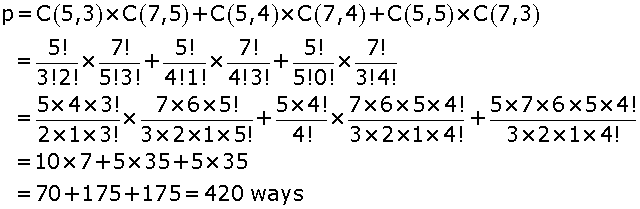
B1, B2, B3, B4, W1, W2 and W3 respectively.
Case 1: When the coin shows a tail, a ball is drawn from a box containing 4 black and 3 white balls
Sample space, S1 = { TB1, TB2, TB3, TB4, TW1, TW2, TW3}
Case 2: When the coin shows a head, a die is thrown which can have any outcome between 1 and 6.
Sample space, S2 = { H1, H2, H3, H4, H5, H6 }
Total Sample Space, S = { TB1, TB2, TB3, TB4, TW1, TW2, TW3, H1, H2, H3, H4, H5, H6}.
a = 4.
Focus is at (4, 0).
Equation of the directrix is : x = - 4.
Length of latus rectum = 4a
= 4(4)
= 16.
x2/a2 + y2/b2 =1
Since the points (2, 1) and (1, -3) lie on the ellipse, we have
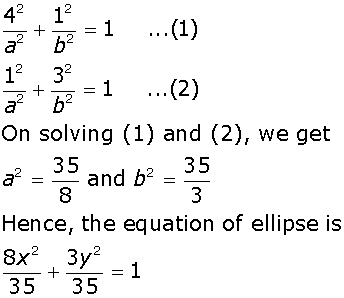
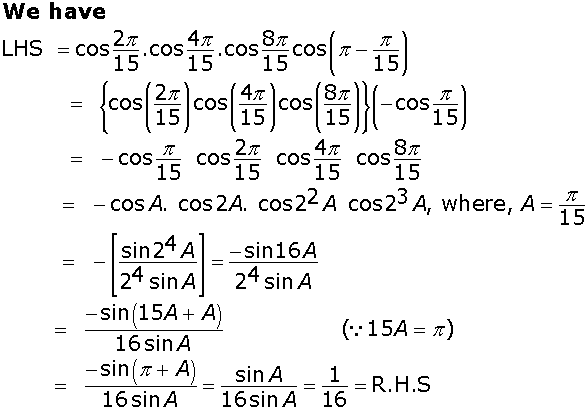
Prove that ![]()

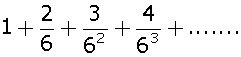
The sum and sum of squares corresponding to height x (in cm) and weight y (in gram) of 50 plant products are given below:
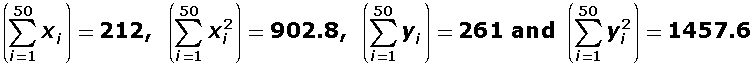
Which is more varying, the height or weight?
| Class | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 |
| Frequency | 7 | 15 | 6 | 16 | 2 | 4 |
| Class | Frequency, f | Cumulative Frequency(c.f) | Mid-point,x |
|
| |
| 0-10 | 7 | 7 | 5 | -20 | 20 | 140 |
| 10-20 | 15 | 22 | 15 | -10 | 10 | 150 |
| 20-30 | 6 | 28 | 25 | 0 | 0 | 0 |
| 30-40 | 16 | 44 | 35 | 10 | 10 | 160 |
| 40-50 | 2 | 46 | 45 | 20 | 20 | 40 |
| 50-60 | 4 | 50 | 55 | 30 | 30 | 120 |
|
| 50 |
|
|
|
|
|
The class-interval containing (N/2)th or 25th item is 20-30. Therefore, it is the
median class.
Here, l = 20, N = 50, C = 22, f= 6 and h = 10
![]()
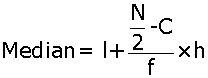 = 20+{(50/2 - 22)}/6
= 20+{(50/2 - 22)}/6 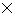 10=25
10=25
M.D.( ![]() ) =
) = 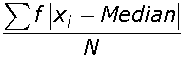 = 610/50= 12.2
= 610/50= 12.2

Take your CBSE board preparation to another level with AI based and rich media animation on Extramarks - The Learning App.
Features of Learning App