

The distance of a point (2, 5) from X-axis is
5 units.
If the distance between points (p, –7),(9, –7) is 15 units, then p is
– 6 or 24.
If 7 is the mean of 5, 3, .5, 4.5, b, 8.5, 9.5, then the value of b is
18
Which of the following is the HCF of two consecutive natural numbers?
1
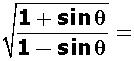
sec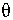 + tan
+ tan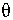 .
.
The value of sin 15° =
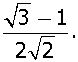
The greatest number which divides 258 and 323 leaving remainders 2 and 3 respectively is
64
The coordinates of the centre of a circle Which is passing through (1, 2),(3, –4) and (5, –6) is
(11, 2)
The lines y = 4x – 10 and y = 7x + 11 intersect at
(-7, -38).
If the roots of quadratic equation 3x2 – 2x – k = 0, are real and equal, then value of k is _____.
If x2 – 3x – 18 = 0, then the roots of quadratic equation are 6 and ____.
If the first term of an AP is ‘x’ and the common difference is ‘y’, then the nth term of the series is _________.
If the first term and common difference of an AP be ‘a’ and ‘d’ respectively, then nth term of AP is:
Tn = a + (n – 1)d
Here, a = x and d = y
Then, for the given series, the nth term is:
Tn = x + (n – 1)y
Therefore, if the first term of an AP is ‘x’ and the common difference is ‘y’,
then the nth term of the series is x + (n – 1)y.
If the sides of two similar triangles are in the ratio 3:4, then the areas of these triangles are in the ratio_____.
The radii of the ends of a frustum of a cone 35 cm high are 7 cm and 4 cm. The volume of the frustum is______.
A number is chosen at random from the numbers –8, –7, –6, –5, –4, –3, –2, –1, 0, 1, 2, 3, 4, 5, 6, 7, and 8. If the selected number is a positive multiple of 3, then the probability of the selected number is ________.
 5?
5? 5 is 2 -
5 is 2 - 5.
5. 3x2 - 3x + x - 1 = 0
3x2 - 3x + x - 1 = 0 3x(x - 1) + (x - 1) = 0
3x(x - 1) + (x - 1) = 0 (x - 1)(3x + 1) = 0
(x - 1)(3x + 1) = 0 x = 1 and x = -1/3
x = 1 and x = -1/3Let three numbers in an AP are a –d, a, a + d.
Therefore, a – d + a + a + d = 15
3a=15
a = 5
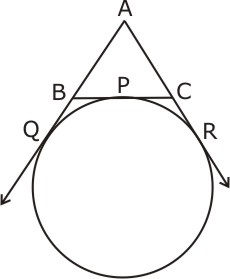
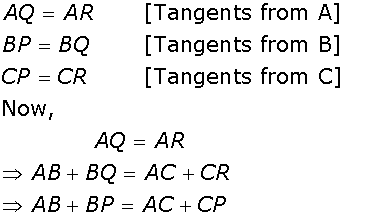
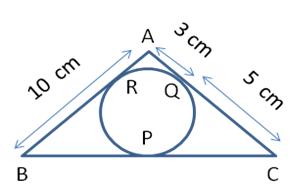
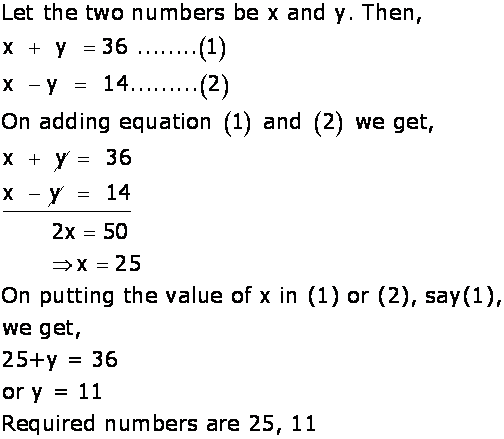
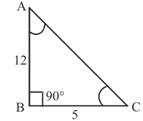
 ABC is right angled at B and
ABC is right angled at B and  A =
A =  C. Is cosA = cosC?
C. Is cosA = cosC?

 C = 3
C = 3 B = 2(
B = 2( A +
A +  B). Find the three angles.
B). Find the three angles.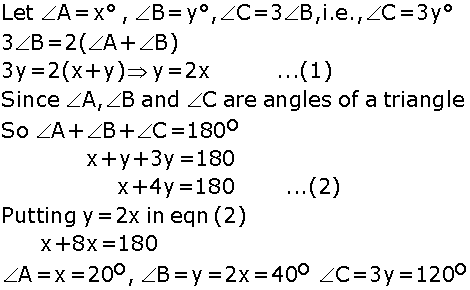
(2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6)
(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6)
(4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6)
(5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6)
(6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)
Total events = 6 x 6 = 36
Favourable event is when the sum is 8.
(2, 6), (3, 5), (4, 4), (5, 3), (6, 2)
Favourable events = 5
Hence, probability of getting 8 as a sum = 5/36
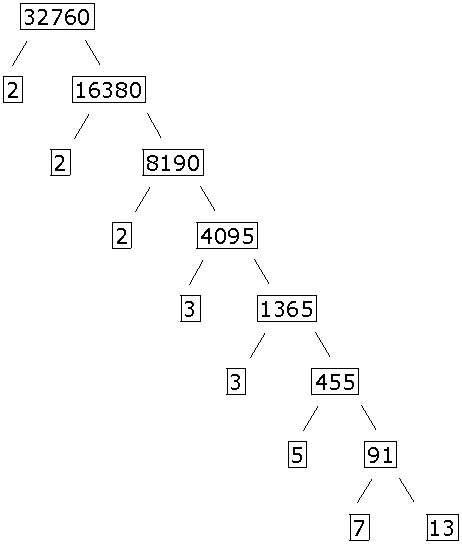
So, we have 32760 = 2  2
2  2
2 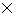 3
3 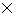 3
3 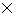 5
5 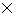 7
7  13
13
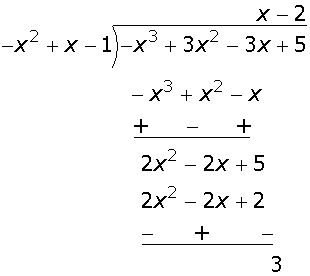
So quotient = x - 2, remainder = 3
Divisor  Quotient + Remainder
Quotient + Remainder ![]()
= (-x2 + x - 1) (x - 2) + 3
= -x3 + 3x2 - 3x + 5 = Dividend
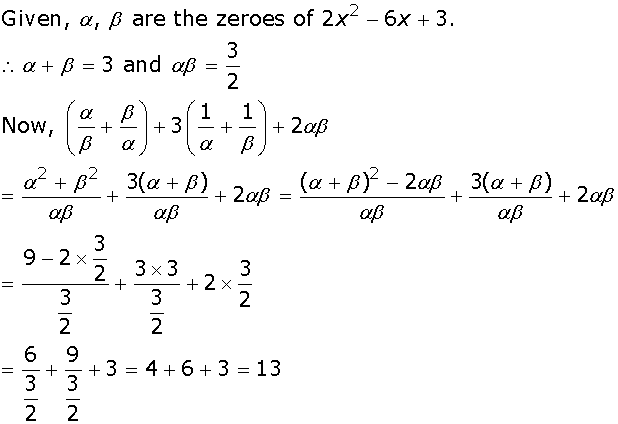

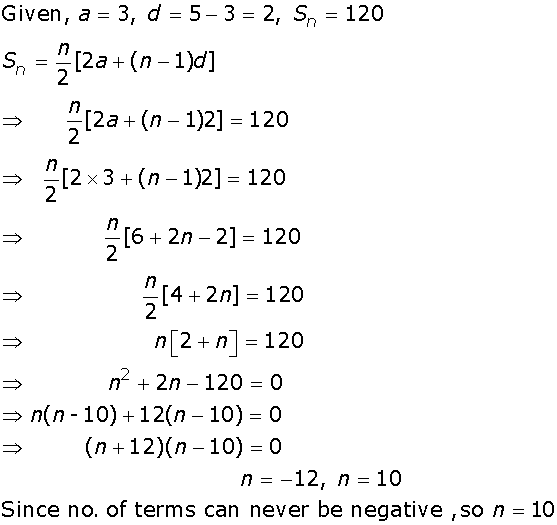
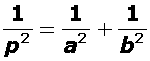
(i) Let CD  AB. Then, CD = p
AB. Then, CD = p
![]() Area of
Area of  ABC = (AB
ABC = (AB  CD)/2 = cp/2 ...(1)
CD)/2 = cp/2 ...(1)
Also,
Area of  ABC = (BC
ABC = (BC  AC)/2 = ab/2 ...(ii)
AC)/2 = ab/2 ...(ii)
From (i) and (ii) we have,
cp = ab.
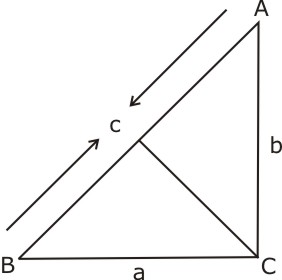
(ii) Since 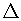 ABC is a right triangle right–angled at C
ABC is a right triangle right–angled at C

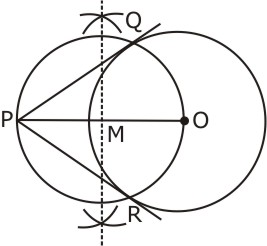
Step 3: Taking M as centre and MO as radius, draw a circle.
Step 4: Let this circle intersect the previous circle at point Q and R.
Step 5: Join PQ and PR. PQ and PR are the required tangents.
| |
| |
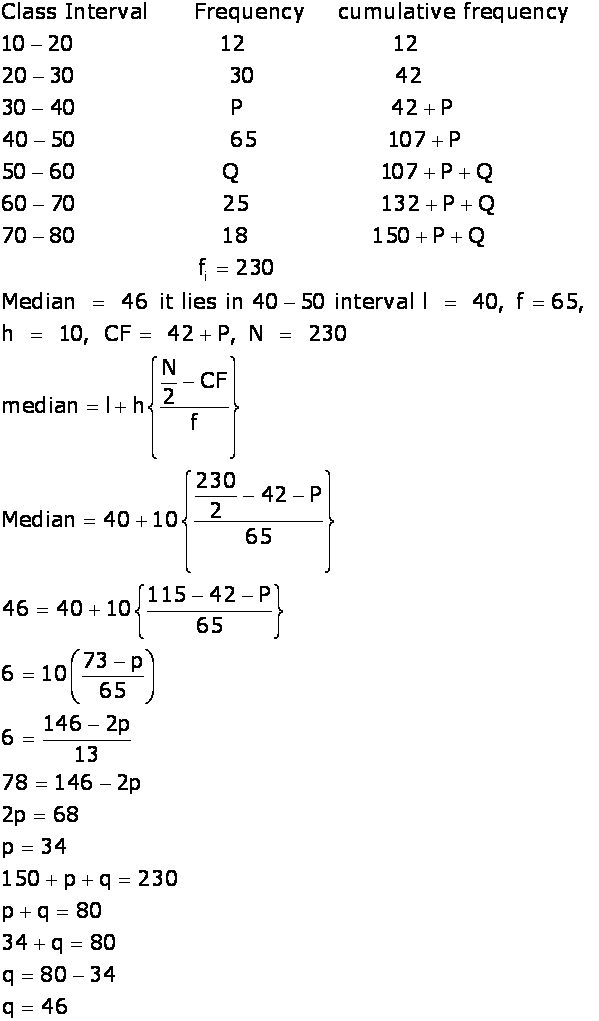
Some students arranged a picnic. The budget for food was Rs.240. Because four students of the group failed to go, the cost of food to each student got increased by Rs 5. How many students went for the picnic?

Let ABCD be the given rectangle and let O be a point within it. Join OA, OB, OC and OD.
Through O, draw EOF || AB. Then, ABFE is a rectangle
In right triangles 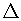 OEA and
OEA and 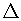 OFC, we have
OFC, we have
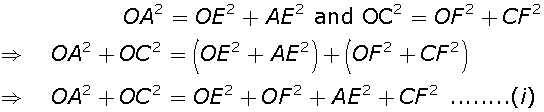
Now, in right triangles  OFB and
OFB and  ODE, we have
ODE, we have
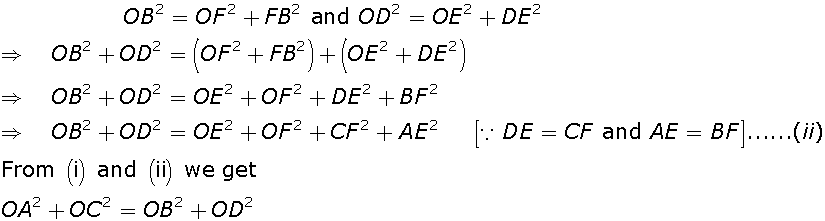
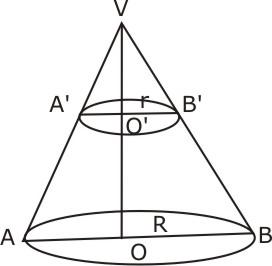
Let VAB be a hollow cone of height H, slant height L and the base radius R.
Suppose this cone is cut by a plane parallel to the base such that O' is the centre of the circular section of the cone.
Let h be the height, l be the slant height and r be the base radius of the smaller cone VA'B'.
In 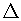 VO’A’ and
VO’A’ and 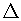 VOA
VOA
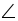 A =
A = 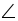 A’
A’
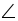 O =
O = 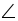 O’
O’
Therefore by AA postulate
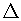 VO’A’
VO’A’ 
 VOA
VOA
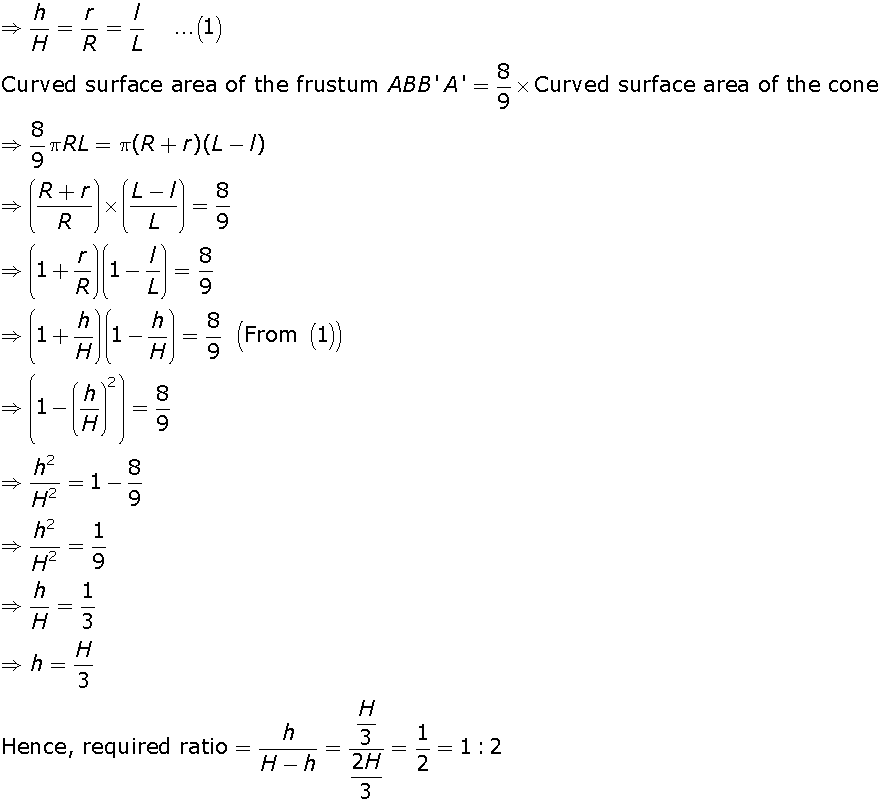
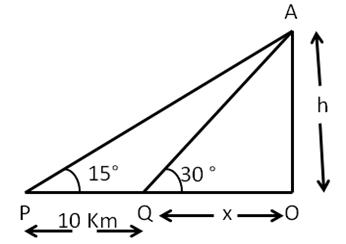
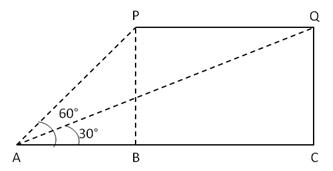
Let AB be a mountain of height h metres and angle of elevation of its top is 30° from a point at x km away from mountain and that of 15° from (x+10)km away from the base of the mountain.
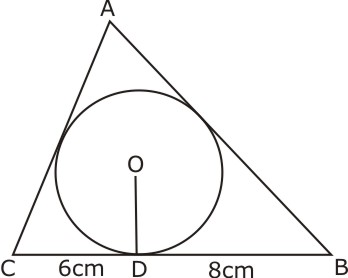
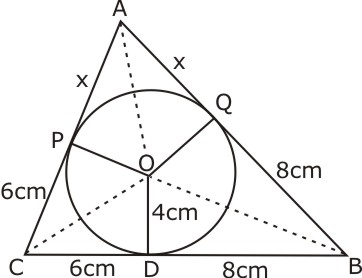

Take your CBSE board preparation to another level with AI based and rich media animation on Extramarks - The Learning App.
Features of Learning App