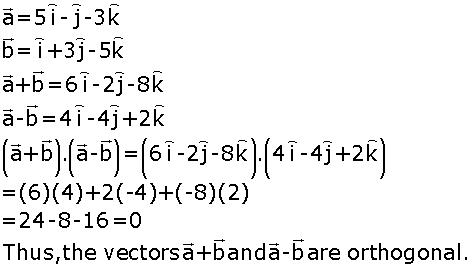CBSE [Delhi]_XII_Mathematics_2004_Set I
To Access the full content, Please Purchase
-
Q1
 Marks:3View Answer
Marks:3View AnswerAnswer:
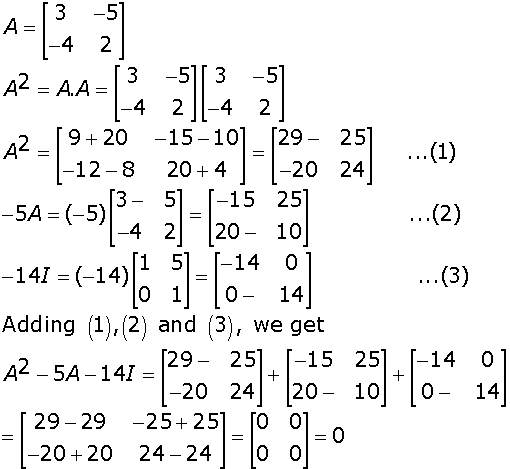
-
Q2
Using properties of determinants solve for x: 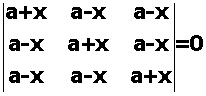 Marks:3View Answer
Marks:3View AnswerAnswer:
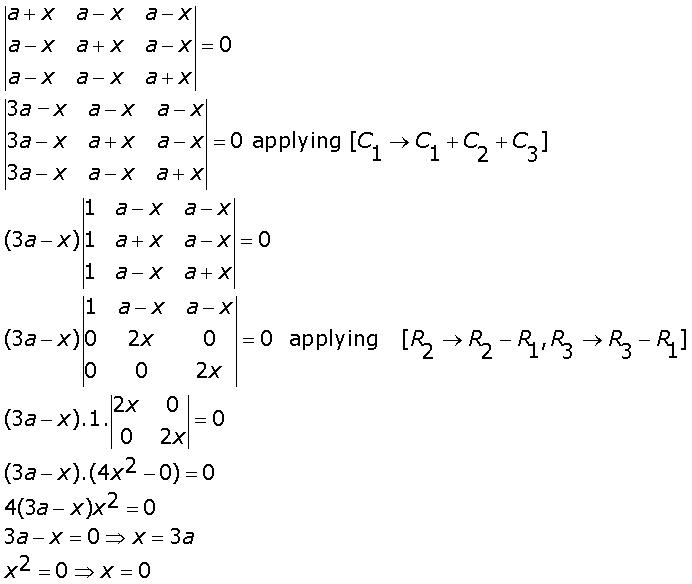
-
Q3
An urn contains 7 white, 5 black and 3 red balls. Two balls drawn at random. Find the probability that
(i) Both the balls are red
(ii) One ball is red, the other is black
(iii) One ball is whiteMarks:3View AnswerAnswer:
Total number of balls = 7(white) + 5(black) + 3(red) = 15
Two balls are drawn out of 15 balls in 15C2 ways.
Let us define the events as follows:(i) A = Both the balls are red There are 3 red balls out of which 2 red balls can be drawn in 3C2 ways. Thus, P(A) = 3C2 /15C2 =1/35.
(ii) B = Two balls are drawn, out of them one ball is red and the other is blackThere are 3 red balls and 5 black balls out of which one ball drawn is red and the other ball drawn is black in 3C1 x 5C1 ways. Thus, P(B) = 3C1 x 5C1/ 15C2 = 1/7.
(iii) C = Two balls are drawn, out of them one ball is white.There are 7 white balls and 8 non-white balls. Two balls are drawn out of them one ball is white and the other ball is non-white in 7C1 x 8C1 ways. Thus, P(C) = 7C1 x 8C1/ 15C2 = 8/15. -
Q4
A fair die is tossed twice. If the number appearing on the top is less than 3, consider it as a success and find the probability distribution of number of successes. Marks:3View AnswerAnswer:
Let X denote the number of successes when a fair die is tossed twice. Then X is a random variable that can take the values 0, 1 or 2.
Probability that a number appearing on the top is less than 3 in a single throw of a dice = Probability of a success = 2/6= 1/3. Probability of not getting a success = 1-1/3= 2/3 P( X = 0) = P( no success) = (2/3)(2/3)= 4/9 P( X = 1) = P(one success ) = (1/3) (2/3)+(1/3)(2/3) = 4/9 P( X = 2) = P( two success) =(1/3)(1/3)= 1/9 -
Q5
Evaluate: 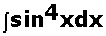 Marks:3View Answer
Marks:3View AnswerAnswer:
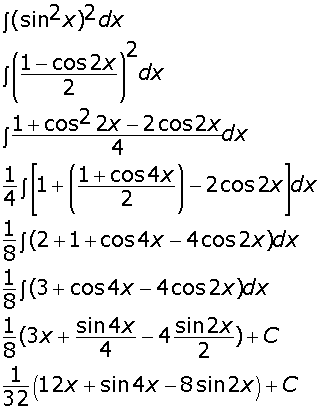
-
Q6
Evaluate: 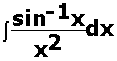 Marks:3View Answer
Marks:3View AnswerAnswer:

-
Q7
Form the differential equation corresponding to y2 = a(b -x2) where a and b are arbitrary constants. Marks:3View AnswerAnswer:
Given y2 = a(b -x2) ...(1) Differentiating with respect to x, we get
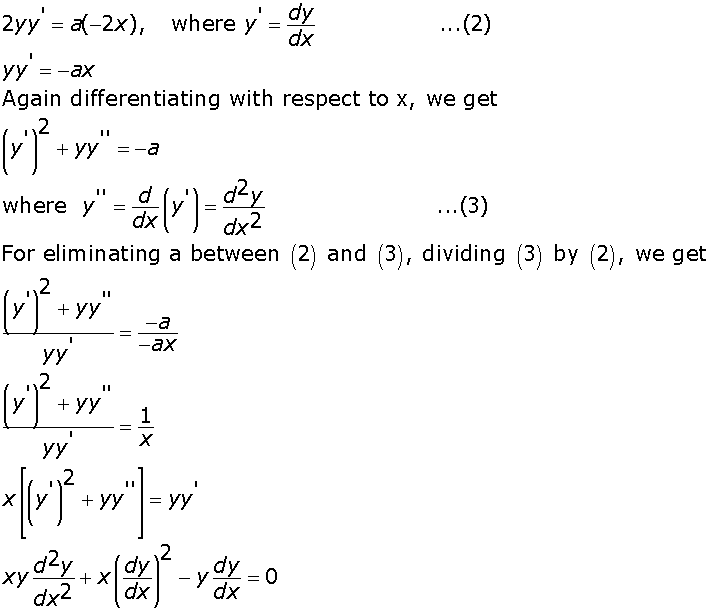
-
Q8
Solve the differential equation:
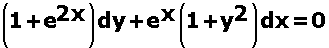 given that when x =0, y =1.
Marks:3View Answer
given that when x =0, y =1.
Marks:3View AnswerAnswer:
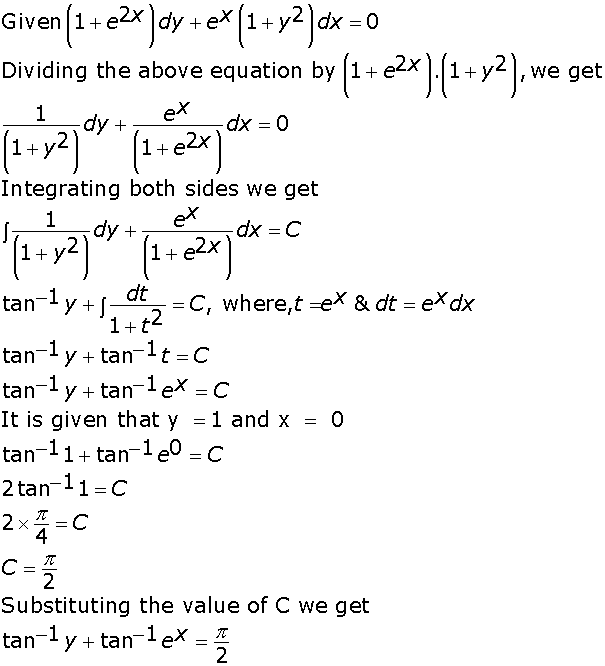
-
Q9
Solve the differential equation: 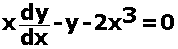 Marks:3View Answer
Marks:3View AnswerAnswer:

-
Q10
 Marks:3View Answer
Marks:3View AnswerAnswer: