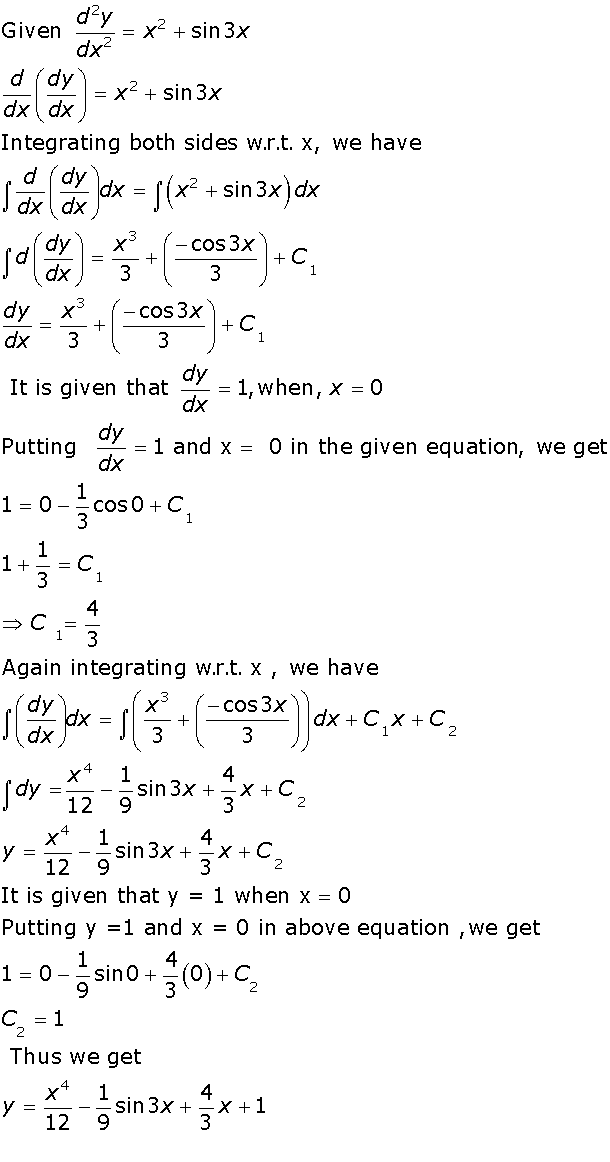CBSE[All India]_XII_Mathematics_2004_Set I
To Access the full content, Please Purchase
-
Q1
The Cartesian equations of a line are 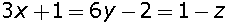 . Find the fixed point through which it passes, its direction ration ratios and also its vector equation.Marks:3View Answer
. Find the fixed point through which it passes, its direction ration ratios and also its vector equation.Marks:3View AnswerAnswer:
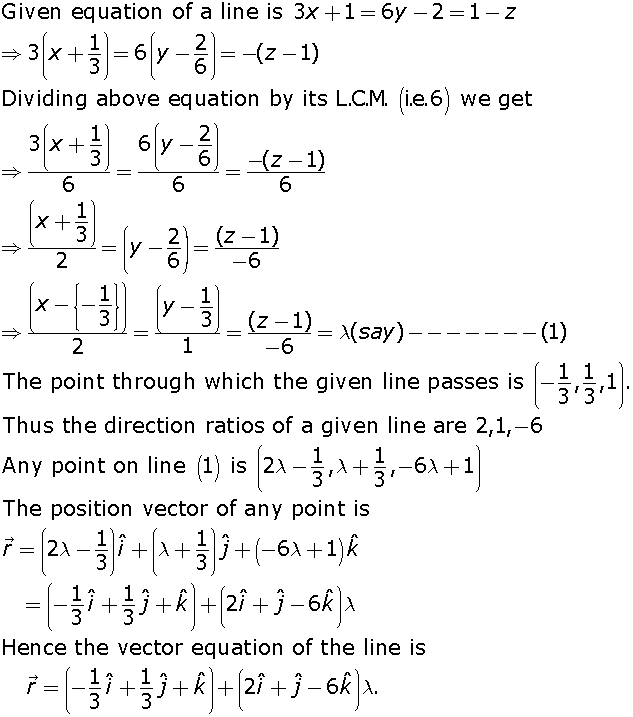
-
Q2
 Marks:3View Answer
Marks:3View AnswerAnswer:
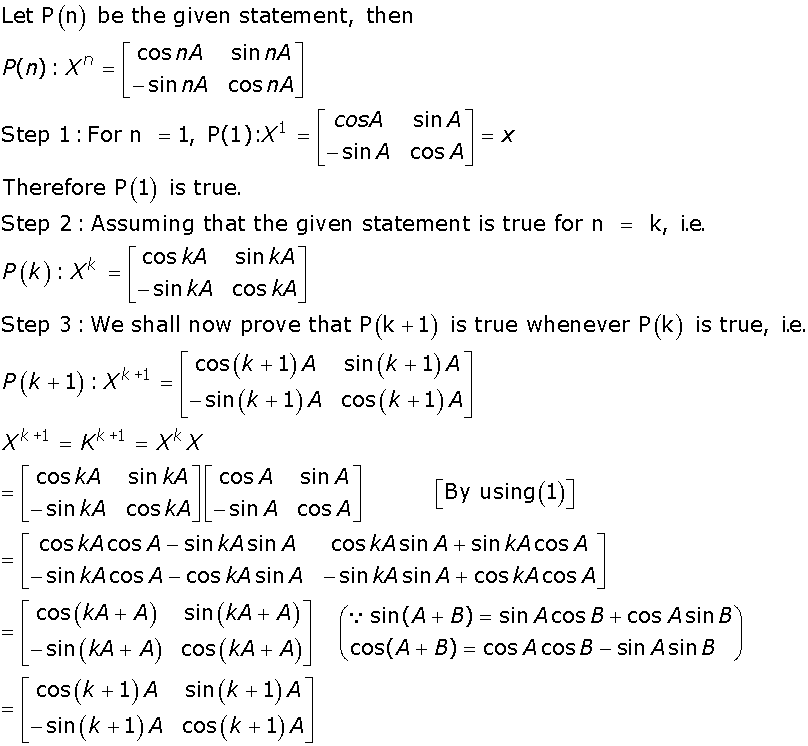
-
Q3
Using properties of determinants, prove that
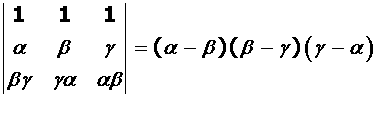
Marks:3View AnswerAnswer:
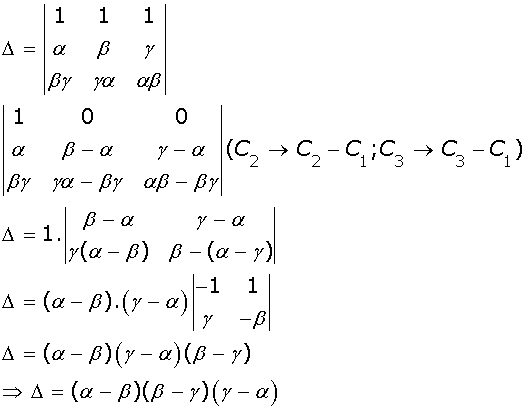
-
Q4
From a bag containing 20 tickets, numbered from 1 to 20. Two tickets are drawn at random. Find the probability that
(i) Both the tickets have prime numbers on them;
(ii) On one there is prime number and on the other there is a multiple of 4.Marks:3View AnswerAnswer:
Total no. of tickets in a bag = 20 2 tickets can be drawn out of 20 in 20C2 ways So exhaustive no. of cases = 20C2= (20)(19)/2 = 190 ways
(i) there are 8 prime numbers from 1 to 20 (i.e. 2,3,5,7,11,13,17,19)Out of these 8 prime numbers, 2 prime numbers can be drawn in 8C2ways. Favorable no. of cases = 8C2= (8) (7)/2 =28
Thus the probability that both the tickets have prime number on them
= Favorable number of cases/ Total number of cases
= 8C2/ 20C2= 28/190 = 14/95
(ii) There are 8 prime numbers from 1 to 20 (i.e. 2,3,5,7,11,13,17,19) and 5 numbers which are multiple of 4 from 1 to 20 Out of these 8 prime numbers and 5 multiples of 4, 1prime number and 1 multiple of 4 can be drawn in 8C1 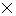 5C1ways
5C1waysFavorable no. of cases = 8C1 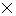 5C1=
5C1=8 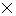 5 = 40 ways
5 = 40 waysThus the probability that one of the tickets has prime number and other has a multiple of 4
= Favorable number of cases/ Total number of cases = 8C15C1/20C2= 40/190 = 4/95 -
Q5
Two dice are tossed once. Find the probability of getting an even number on the first dice or a total of 8. Marks:3View AnswerAnswer:
Let S be the sample space associated with the experiment when two dice are tossed once. Then, n(S) = 62 = 36 Let A = Getting a even number on the first dice B = Getting a total of 8 A 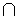 B= Getting an even number on the first dice and a total of 8.
B= Getting an even number on the first dice and a total of 8.A = {(2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6), (6, 1), (6, 2),(6, 3), (6, 4), (6, 5), (6,6)}
n(A) = 18 B = {(2, 6), (3, 5), (4, 4), (5, 3), (6, 2)} n(B) = 5 A 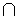 B= {(2, 6), (4, 4), (6, 2)}
B= {(2, 6), (4, 4), (6, 2)}n( A 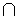 B) = 3
B) = 3P(A) = n(A)/n(S) = 18/36 P(B) = n(B)/n(S)= 5/36 P( A 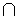 B) =
B) =n(A 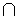 B) /n(S)= 3/36
B) /n(S)= 3/36
Required probability:P( A 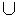 B) = P(A) + P(B) - P(
B) = P(A) + P(B) - P(A 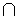 B)
B)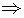 18/36 +5/36 -3/36 = 20/36 = 5/9
18/36 +5/36 -3/36 = 20/36 = 5/9 -
Q6
From a lot of 30 bulbs, which includes 6 defective bulbs, a sample of 3 bulbs is drawn at random with replacement. Find the probability distribution of the number of defective bulbs. Marks:3View AnswerAnswer:
As X denote the number of defective bulbs in the sample space, therefore X can take the values of 0,1,2,3. Total numbers of bulb in the lot = 30= 6 defective bulbs +24 non defective bulbs Probability of getting a defective bulb = 6/30 =1/5 Probability of getting a non defective bulb = 24/30= 4/5 P(X=0)=P( no defective bulbs)

Thus, the probability distribution is X 0 1 2 3 P(X) 64/125 48/125 12/125 1/125 -
Q7
Evaluate 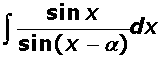 .
Marks:3View Answer
.
Marks:3View AnswerAnswer:
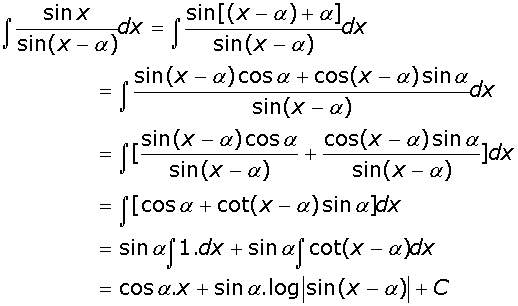
-
Q8
Evaluate 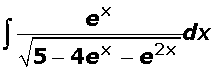 .
.
Marks:3View AnswerAnswer:
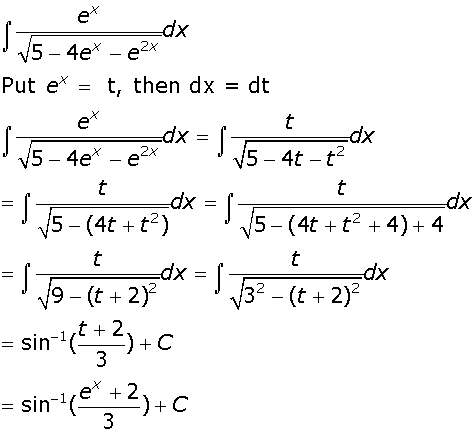
-
Q9
Solve the differential equation 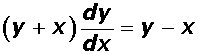 .Marks:3View Answer
.Marks:3View AnswerAnswer:
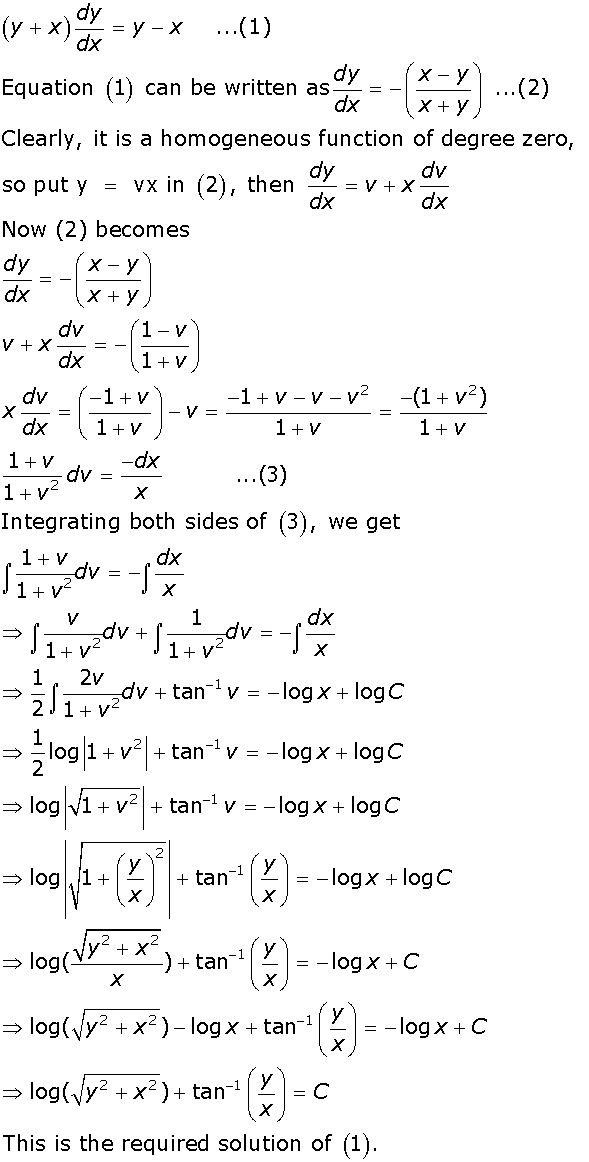
-
Q10
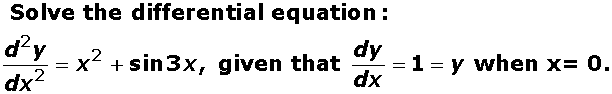 Marks:3View Answer
Marks:3View AnswerAnswer: