CBSE[OUTSIDE DELHI]_X_Mathematics_2019_Set_I
To Access the full content, Please Purchase
-
Q1
Find the value of k for which the quadratic equation kx (x–2) + 6 = 0 has two equal roots.
Marks:1View AnswerAnswer:
The given quadratic equation is:
kx (x–2) + 6 = 0
kx2 – 2kx + 6 = 0
Comparing with ax2 + bx + c = 0, we get
a = k, b = – 2k and c = 6
Since, roots are equal. So,
D = 0 i.e., b2 – 4ac = 0
(–2k)2 – 4k(6) = 0
4k2 – 24k = 0
4k(k – 6) = 0
Either k = 0 (Neglect)
Or k = 6
Therefore, the value of k is 6.
-
Q2
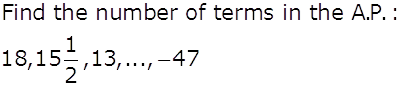 Marks:1View Answer
Marks:1View AnswerAnswer:

-
Q3
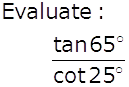 Marks:1View Answer
Marks:1View AnswerAnswer:
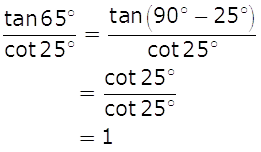
-
Q4
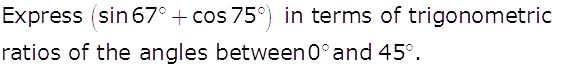 Marks:1View Answer
Marks:1View AnswerAnswer:
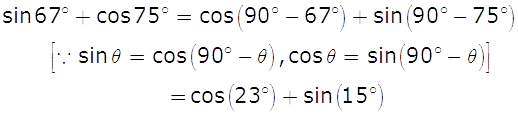
-
Q5
 Marks:1View Answer
Marks:1View AnswerAnswer:

-
Q6
Find the distance between the points (a, b) and
(–a, –b).Marks:1View AnswerAnswer:
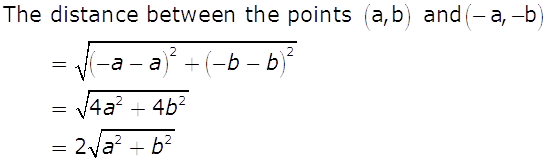
-
Q7
 Marks:1View Answer
Marks:1View AnswerAnswer:

-
Q8
 Marks:1View Answer
Marks:1View AnswerAnswer:
Since, 22 × 53 × 32 × 17 = (2×5)×(2×5)×2×32×17
= 10 × 10 × 2 × 9 × 17
As there are two 10’s. So, number of zeroes in the end of number obtained by given product is two. -
Q9
How many multiples of 4 lie between 10 and 205?
Marks:2View AnswerAnswer:
The multiples between 10 and 205 are:
12, 16, 20, …, 204
Here, first term (a) = 12
and common difference (d) = 4Let an = 204
a + (n – 1) d = 204
12 + (n – 1)3 = 204
(n – 1)3 = 204 – 12
(n – 1) = 192/3
n = 64 + 1
= 65
Therefore, there are 65 multiples of 4 between 10 and 205.
-
Q10
Determine the A.P. whose third term is 16 and 7th term exceeds the 5th term by 12.
Marks:2View AnswerAnswer:
Given: a3 = 16, a7 – a5 = 12
Let first term of AP be ‘a’ and common
difference be ‘d’.Since, an = a + (n – 1)d
So, a3 = a + (3 – 1)d
Or 16 = a + 2d …(i)
a7 – a5 = 12
(a + 6d) – (a + 4d) = 12
2d = 12
d = 6
a + 2(6) = 16
a = 16 – 12
= 4The required AP is:
a, a + d, a + 2d, a + 3d, …
or 4, 4 + 6, 4 + 2(6), 4 + 3(6), …
i.e., 4, 10, 16, 22,…



