CBSE [Delhi]_X_Mathematics_2015_Set II
To Access the full content, Please Purchase
-
Q1
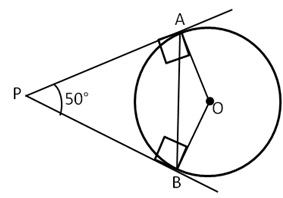
In Fig. 1, PA and PB are tangents to the circle with centre O such that ∠APB=50o. Write the measure of∠OAB.
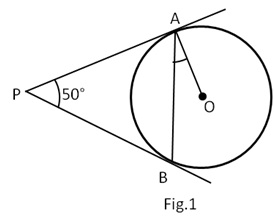Marks:1View AnswerAnswer:
Join OC.
-
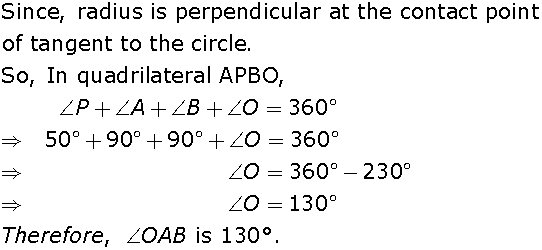
Q2
A letter of English alphabet is chosen at random. Determine the probability that the chosen letter is a constant.
Marks:1View AnswerAnswer:
Number of English alphabet = 26
Number of constants = 21Probability of choosing a constant = 21/26
-
Q3
The tops of two towers of height x and y, standing on level ground, subtend angles of 30° and 60° respectively at the centre of the line joining their feet, then find x:y.
Marks:1View AnswerAnswer:
-
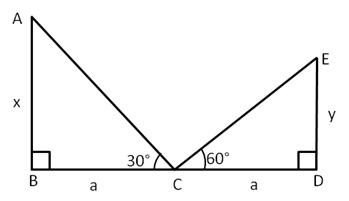
Q4
Marks:1View AnswerAnswer:
-
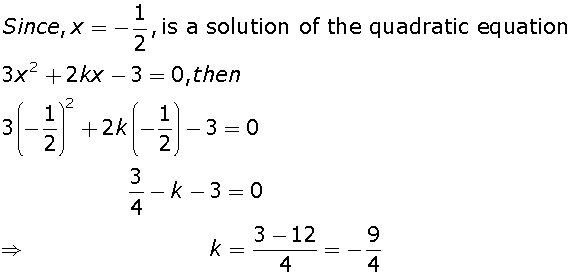
Q5
If A(5, 2), B(2,–2) and C(–2, t) are the vertices of a right angled triangle with angle B = 90°, then find the value of t.
Marks:2View AnswerAnswer:
In right angled triangle, ABC,
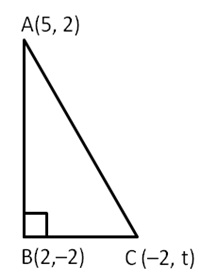
By Pythagoras Theorem,
AC2 = AB2 + BC2
(5 + 2)2 +(2 – t)2 =(5 – 2)2 +(2 +2)2 +(2 + 2)2
+(–2 – t)272 + 4 – 4t + t2 = 9 + 16 + 16 + 4 + 4t + t2
53 – 4t = 45 + 4t
53 – 45 = 8t
t = 8/8 = 1 -
Q6
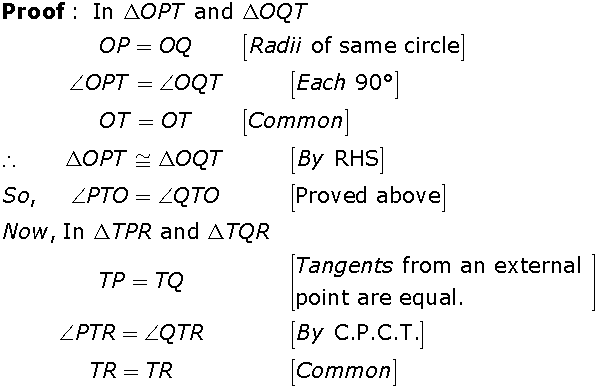
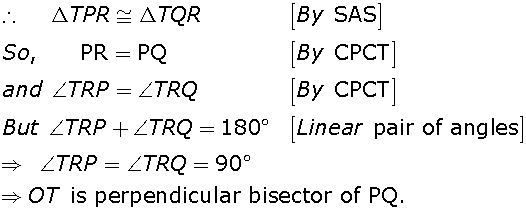
From a point T outside a circle of centre O, tangents TP and TQ are drawn to the circle. Prove that OT is the right bisector of line segment PQ.
Marks:2View AnswerAnswer:
Given: TP and TQ are tangents to circle and OT intersects chord PQ at R.
To Prove: OT bisects PQ at right angle.
-
Q7
In Fig. 2, AB is the diameter of a circle with centre O and AT is a tangent. If
.
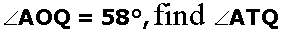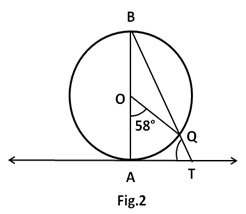Marks:2View AnswerAnswer:
-
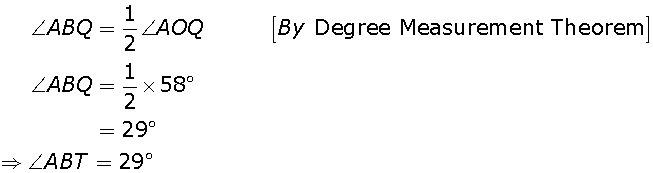
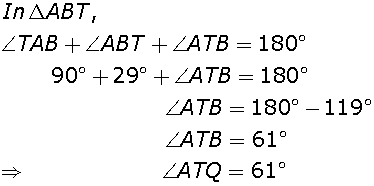
Q8
Solve the following quadratic equation for x:
4x2 – 4a2x + (a4 – b4) = 0
Marks:2View AnswerAnswer:
-
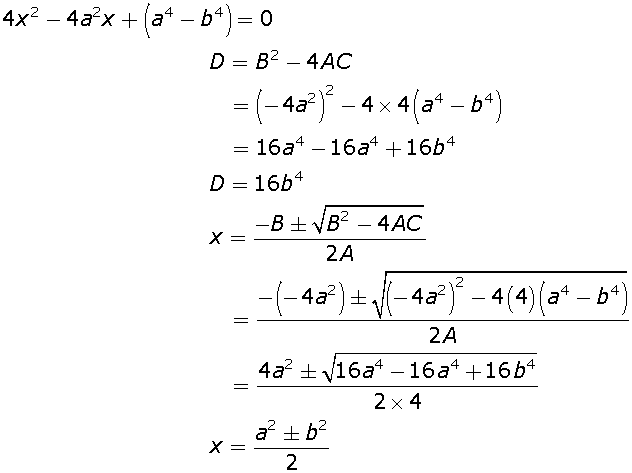
Q9
Marks:2View AnswerAnswer:
-
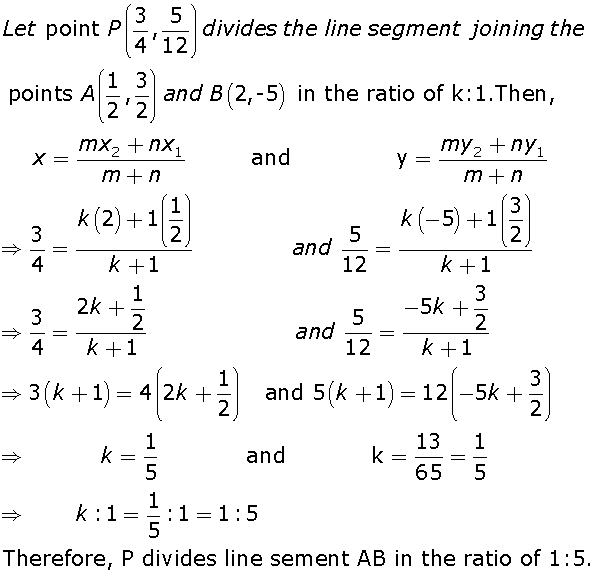
Q10
Find the middle term of the A.P. 213, 205, 197, …, 37.
Marks:2View AnswerAnswer:
Since, l = a + (n – 1)d
Here, a = 213, d = 205 – 213 =– 8 and l = 37So, 37 = 213 + (n – 1)( – 8)
37 = 213 – 8n + 8
n = 23
